Furjė transformacija: savybės, programos, pavyzdžiai ir pratimai
Furjė transformacija yra analitinio pritaikymo metodas, orientuotas į integruotas funkcijas, priklausančias integruotų transformacijų šeimai. Ją sudaro funkcijų f (t) iš naujo apibrėžimas pagal Cos (t) ir Sen (t).
Šių funkcijų trigonometriniai identitetai kartu su jų išvestinėmis ir antideryvacinėmis savybėmis padeda apibrėžti Furjė transformaciją per šią sudėtingą funkciją:

Tai tiesa, kol išraiška yra prasminga, ty kai netinkamas integralas yra konvergencinis. Algebriniu būdu sakoma, kad Furjė transformacija yra linijinis homeomorfizmas.
Bet kokia funkcija, kurią galima apdoroti su Furjė transformacija, turi būti negaliojanti už apibrėžto parametro.
Savybės

Furjė transformacija atitinka šias savybes:
Egzistavimas
Siekiant patikrinti Furjė transformacijos egzistavimą f (t) funkcijoje, apibrėžtoje realuose R, turi būti įvykdytos šios 2 aksiomos:
- f (t) yra nepertraukiamas visiems vienetams
- f (t) yra integruotas į R
Furjė transformacijos linijiškumas
Leiskite M (t) ir N (t) būti bet kokia dviem funkcijomis su apibrėžtomis Furjė transformacijomis, turinčiomis a ir b konstantas.
F [a M (t) + bN (t)] (z) = a F [M (t)] (z) + bF [N (t)] (z)
Kuris taip pat yra pagrįstas to paties pavadinimo vientisumo linijumu.
Išvestinės priemonės Fourier transformacija
Mes turime funkciją f, kuri yra nepertraukiama ir integruota visose realijose, kur:

F (f ') darinys yra nepertraukiamas ir apibrėžtas vienetais per R
Išvestinės priemonės Furjė transformacija apibrėžiama integruojant pagal dalis, pagal šią išraišką:
F [f '(t)] (z) = iz F [f (t)] (z)
Didesnės eilės išvestyse jis bus taikomas homologiškai, kur visiems n 1:
F [f n '(t)] (z) = (iz) n F [f (t)] (z)
Furjė transformacijos diferencijavimas
Mes turime funkciją f, kuri yra nepertraukiama ir integruota visose realijose, kur:
i (d / dz) F [f (t)] (z) = F [t. f (t)] (z)
Vertimo Furjė transformacija
Visam θ, kuris priklauso S ir T rinkiniui, kuris priklauso S rinkiniui, jis turi:
F [ τ a θ] = e-iay F [ θ] F [ τ a T ] = e-iax F [ T]
Su τ a veikia kaip vertimo operatorius vektoriuje a.
Furjė transformacijos vertimas
Visam θ, kuris priklauso S ir T rinkiniui, kuris priklauso S rinkiniui, jis turi:
τ a F [θ] = F [e-x . θ] τ a F [T ] = F [e-iay . T]
Visiems, kurie priklauso R
Skalės grupės Fourier transformacija
Visam θ, kuris priklauso rinkiniui S. T, kuris priklauso rinkiniui S '
λ, priklausantis R - {0}, turite:
F [θ (λx)] = (1 / | λ |) F [θ] ( y / λ )
F [T (λx)] = (1 / | λ |) F [T] (y / λ )
Jei f yra nuolatinė ir aiškiai integruota funkcija, kur a> 0. Tada:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Norėdami parodyti šį rezultatą, galite keisti kintamąjį.
Kai T → + tada s = ne → + ∞
Kai T → - tada s = ne → - ∞



Simetrija
Norėdami ištirti Furjė transformacijos simetriją, turi būti patikrinta Parseval tapatybė ir Plancherel formulė.
Mes turime θ ir δ, kurie priklauso S. Iš ten galima daryti išvadą, kad:

Gauti
1 / (2π) d { F [θ ], F [δ ] } „Parseval“ tapatybė
1 / (2π) d / 2 || F [θ ] || Plancherel L 2 R d formulė
Ketvirtojo konvertavimo produkto transformacija
Pagal panašius tikslus, kurie Laplaso transformacijoje, funkcijų konvoliucija reiškia produktą tarp jo Fourier transformacijų.
Turime f ir g kaip 2 ribotas, apibrėžtas ir visiškai integruotas funkcijas:
F (f * g) = F (f). F (g)


Tada keičiant kintamąjį
t + s = x; tęsiasi su netinkamu dvigubu integralu



F (f). F (g) = F (f. G)
Tęstinumas ir begalybė
Visiems θ, kurie priklauso R, F [ θ] laikosi nuolatinės funkcijos, apribotos Rd.
Taip pat { F [ θ] (y)} → 0 C, jei | y | → ∞
Istorija
Šią matematinę koncepciją 1811 m. Pristatė Džozefas B. Furjė, kurdamas šilumos sklaidos traktatą . Ją greitai priėmė įvairios mokslo ir inžinerijos šakos.
Ji buvo sukurta kaip pagrindinė darbo priemonė dalinių diferencialinių lygčių tyrimui, net lyginant su darbo santykiais tarp Laplaso transformacijos ir paprastųjų diferencialinių lygčių.
Kam naudojamas „Fourier“ transformavimas?
Juo daugiausia siekiama žymiai supaprastinti lygtis, o išvestines išraiškas paverčiant galios elementais, o tai reiškia diferencines išraiškas integruotų polinomų forma.
Optimizuojant, moduluojant ir modeliuojant rezultatus, tai yra standartizuota išraiška, kuri yra dažnas šaltinis inžinerijai po kelių kartų.
„Fourier“ serija
Jie yra serijos, apibrėžtos pagal kosines ir krūtis; jie padeda palengvinti darbą su bendromis periodinėmis funkcijomis. Taikant, jie yra dalinių ir paprastų diferencialinių lygčių sprendimo būdų dalis.
„Fourier“ serijos yra dar bendresnės nei „Taylor“ serijos, nes jos kuria periodines nenutrūkstamas funkcijas, kurios neturi reprezentacijos „Taylor“ serijoje.
Kitos Fourier serijos formos
Norint suprasti Furjė transformaciją analitiškai, svarbu peržiūrėti kitas formas, kuriose galima rasti „Fourier“ seriją, kol negalime apibrėžti „Fourier“ serijos savo sudėtinėje žymoje.
- „Fourier“ serijos 2L periodo funkcijai
Daug kartų būtina pritaikyti „Fourier“ serijos struktūrą periodinėms funkcijoms, kurių laikotarpis yra p = 2L> 0 intervale [-L, L].
- Furjė serijos nelygios ir lygios funkcijos
Laikoma, kad intervalas [-π, π] suteikia pranašumų naudodamas simetriškas funkcijų savybes.
Jei f yra lygus, „Fourier“ serija yra sukurta kaip „Cosines“ serija.

Jei f yra nelyginis, „Fourier“ serija yra sukurta kaip „Sines“ serija.

- Užpildytas „Fourier“ serijos žymėjimas
Jei turime funkciją f (t), kuri atitinka visus reikalavimus, keliamus Fourier serijos plėtrai, galima pažymėti ją intervalu [-t, t], naudojant sudėtingą žymėjimą:

Programos

Pagrindinio sprendimo apskaičiavimas
Furjė transformacija yra galingas įrankis tiriant dalinės diferencialinės lygtys linijinio tipo su pastoviais koeficientais. Jie vienodai taikomi su ribotomis sritimis.
Kaip ir Laplaso transformacija, Furjė transformacija paverčia dalinę išvestinę funkciją į paprastą diferencialinę lygtį, kuri yra daug paprastesnė.
Šilumos lygties Cauchy problema rodo dažną Furjė transformacijos taikymo sritį, kur generuojama pagrindinė šilumos funkcija arba Dirichlet branduolys.
Kalbant apie pagrindinio sprendimo apskaičiavimą, pateikiami tokie atvejai, kai yra paprasta rasti „Fourier“ transformaciją:
- Laplaso pareikalavimas
- šilumos išsiskyrimas
- Šrödingerio miestas
- bangų išraiška
Signalo teorija
Bendra priežastis, kodėl šioje šakoje naudojama Fourier transformacija, yra daugiausia dėl to, kad signalas yra būdingas, kaip begalinis lengviau apdorojamų signalų superpozicija.
Tai gali būti garso banga arba elektromagnetinė banga, Furjė transformacija ją išreiškia paprastų bangų superpozicijoje. Šis vaizdavimas yra gana dažnas elektros inžinerijoje.
Kita vertus, yra Fourier transformacijos taikymo signalų teorijos srityje pavyzdžiai:
- Sistemos identifikavimo problemos. Nustatyta fyg
-Problema su išvesties signalo nuoseklumu
- Problemos, susijusios su signalo filtravimu
Pavyzdžiai
1 pavyzdys
Nustatykite Furjė transformaciją šiai išraiškai:

Taip pat galime jį atstovauti taip:
F (t) = Sen (t) [H (t + k) - H (t - k) ]
Apibrėžtas stačiakampis pulsas:
p (t) = H (t + k) - H (t - k)
Furjė transformacija taikoma tokiai išraiškai, kuri yra panaši į moduliacijos teoriją.
f (t) = p (t) Sen (t)
Kur: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Ir Furjė transformaciją apibrėžia:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
2 pavyzdys
Apibrėžkite Furjė transformaciją:


Kadangi f (h) yra lygi funkcija, tai galima pasakyti


Integracija dalimis taikoma taikant kintamuosius ir jų skirtumus
u = sin (zh) du = z cos (zh) dh
dv = h (eh) 2 v = (eh) 2/2
Pakeisti turite

Įvertinus pagal pagrindinę skaičiavimo teoriją

Taikant ankstesnes žinias apie pirmosios eilės diferencialines lygtis, išraiška žymima kaip

Norėdami gauti K vertiname

Galiausiai, frazės Furjė transformacija yra apibrėžiama kaip

Siūlomi pratimai
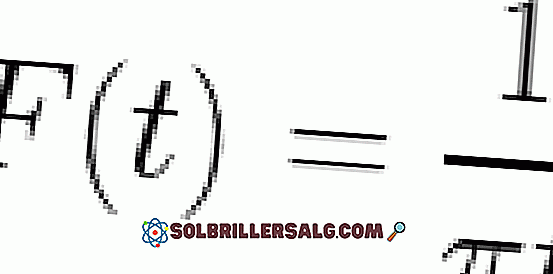

- Gaukite išraiška W / (1 + w2)









